Question

Suppose that the ages of members in a large billiards league have a known standard deviation of σ = 12 σ=12sigma, equals, 12 years. Hernando plans on taking a random sample of n nn members from this population to make a 95 % 95%95, percent confidence interval for the mean age in the league. He wants the margin of error to be no more than 5 55 years. Which of these is the smallest approximate sample size required to obtain the desired margin of error?

Answer 1

`n\geq 23`

Explanation:

-For a known standard deviation, the sample size for a desired margin of error is calculated using the formula:

`n\geq ((z\sigma)/(ME))^2`

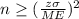
Where:

• 
  `\sigma` is the standard deviation
• 
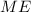  `ME` is the desired margin of error.

We substitute our given values to calculate the sample size:

`n\geq ((z\sigma)/(ME))^2\\\\\geq ((1.96* 12)/(5))^2\\\\\geq 22.13\approx23`

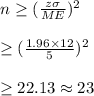
Hence, the smallest desired sample size is 23