Answer:
Sue's percentage profit = 9% on each tin of green paint she sells.
Step-by-step explanation:
Litres of green paints mixed = 50 litres
Ratio of litres of yellow paint and litres of blue paint = 1:4.
To determine the litres of yellow paint, we say:
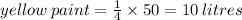
To determine the litres of blue paint, we say:
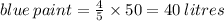
Since yellow paint is sold in 5 litres per tin and each tin cost £38; she has 10 litres of yellow paint in all. That implies that she has 10/5 = 2 tin of yellow paint. If one tin cost £38; 2 tin cost 2 × £38 = £76
Similarly,
Since blue paint is sold in 10 litres per tin and each tin cost £58; she has 40 litres of blue paint in all. That implies that she has 40/10 = 4 tin of blue paint. If one tin cost £58; 4 tin cost 4 × £58 = £232
Total cost of yellow and blue paints = £232 + £76
= £308
Since Sue sells all the green paint she makes in 10 litre tins at £89.32 per tin and she has 50 litres in all; we say: 50/10 litres = 5 tins = 5 × £89.32 = £446.60.
Thus, selling price of the green paint = £446.60

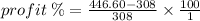
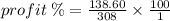
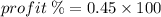
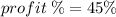
Sue's percentage profit for selling all the tins of green paint is 45%, having sold 5 tins. Therefore, Sue's percentage profit for selling each of the paint will be:
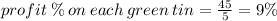
Hence, Sue's percentage profit for selling each tin of green paint is 9%.
Proof
9% × 5 tins of green paint = 45%