Question

You invest $500 in an account that has an annual interest rate of 8%, compounded weekly for 12 years. What is the equivalent interest rate and how many times will the money be compounded? How much will you have?

Answer 1

8% annual interest rate when compounded weekly =

(1 + .08/ 52)^52 = 1.00153846153846154^52 = 1.08322047419671 =

8.322047419671% equivalent interest rate

In 12 years this will be compounded 624 times

12 year Total = 500 * (1.08322047419671)^12 =

1,304.8852611583 =

1,304.89 (rounded)

Answer 2

`i_m=8.322\%\\\\624 \ compoundings\\\\A_(12)=\$1,304.88`

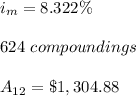
Explanation:

#The equivalent interest rate per annum is equal to the effective interest rate.

-Given 8% compounded weekly( Take 1 yr=52 weeks) the effective interest rate is calculated as:

`i_m=(1+i/m)^m-1\\\\\#where\\i=stated \ interest\ rate\\m=number \ of \ compoundings \ per \ year\\\\\therefore i_m=(1+0.08/52)^(52)-1\\\\=0.08322\approx 8.322\%`

Hence, the equivalent interest rate is 8.322%

-Assuming one year has 52 weeks, the number of compoundings will be :

`=compoundings \ per \ year * \ no \ of \ years\\\\=52* 12\\\\=624\ compoundings`

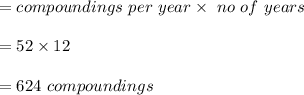
-The investment amount after 12 years is calculated as:

`A=P(1+i_m)^n, n=number \ of \ years\\\\=500(1.08322)^(12)\\\\=1304.88`

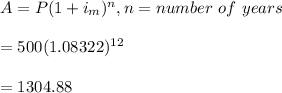
Hence, the amount after 12 years is $1304.88