Given:
m∠WYX = 20°
m∠XYZ = 135°
To find:
The measure of arc WXZ.
Solution:
m∠WYZ = m∠WYX + m∠XYZ
m∠WYZ = 20° + 135°
m∠WYZ = 155°
The measure of inscribed angle is half of the intercepted arc.
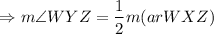
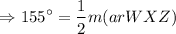
Multiply by 2 on both sides.
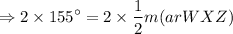
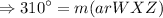
The measure of arc WXZ IS 310°.