Answer:
The coefficient of kinetic friction is

Step-by-step explanation:
Let us call
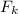 the force of friction, then we know that
the force of friction, then we know that
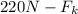 is what has caused the acceleration
is what has caused the acceleration
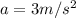 :
:
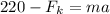
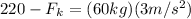
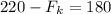

Now this frictional force relates to the coefficient of kinetic friction
 by
by
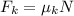
where
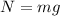 is the normal force.
is the normal force.
Putting in numbers and solving for
 we get:
we get:
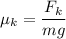
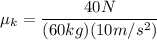
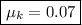
Hence, the coefficient of kinetic friction is 0.07.