Question

Length of the median CP

Answer 1

Given:

ΔABC
`\sim` ΔDEF

To find:

The length of median CP

Solution:

In ΔABC,

AP = 12, BP = 12 and PC = 3x - 12

In ΔDEF,

DQ = 16, QE = 16 and FQ = 2x + 8

If two triangles are similar, then their median is proportional to the corresponding sides.

`$\Rightarrow (AP)/(DQ) =(PC)/(FQ)`

`$\Rightarrow (12)/(16) =(3x-12)/(2x+8)`

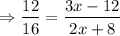
Do cross multiplication.

`$\Rightarrow 12(2x+8)=16(3x-12)`

`$\Rightarrow 24x+96=48x-192`

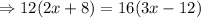
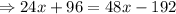
Add 192 on both sides.

`$\Rightarrow 24x+96+192=48x-192+192`

`$\Rightarrow 24x+288=48x`

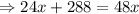
Subtract 24x from both sides.

`$\Rightarrow 24x+288- 24x=48x- 24x`

`$\Rightarrow 288=24x`

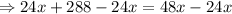
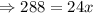
Divide by 24 on both sides.

⇒ 12 = x

Substitute x = 12 in CP.

CP = 3(12) - 12

= 36 - 12

= 24

The length of median CP is 24.