Answer:
The correct answer is a) R = = -
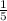
 + 30x; b) $ 1120; c) Maximum quantity is 75 units with maximum revenue being $1125; d) p = $15.
+ 30x; b) $ 1120; c) Maximum quantity is 75 units with maximum revenue being $1125; d) p = $15.
Explanation:
Demand equation: p = -
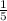 x + 30 , 0
x + 30 , 0
 x
x
 150 ; where p is the price of the product and x is the quantity sold.
150 ; where p is the price of the product and x is the quantity sold.
a) Revenue function by the problem is given to be R= p × x = -
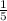
 + 30x.
+ 30x.
b) Revenue at x = 70 is given by 2100 - 980 = $ 1120.
c) For maximizing the R we differentiate it with respect to x and equate it to zero.
⇒ -
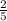 x + 30 =0
x + 30 =0
⇒ x = 75.
As the second order derivative is negative at this point, this is the value of x that maximizes the revenue.
Maximum Revenue is at x = 75 and is equal to $1125.
d) Price charged by the company for maximum revenue is $15.