Question

g The tangent plane to z=f(x,y) at the point (1,2) is z=5x+2y−10. (a) Find fx(1,2) and fy(1,2). fx(1,2)= Number fy(1,2)= Number (b) What is f(1,2)? f(1,2)= Number (c) Approximate f(1.1,1.9). f(1.1,1.9)= Number

Answer 1

The values for Fx(1,2) and Fy(1,2) are 5 and 2 respectively.

Approximation at points (1.1,1.9) is 0.7

Explanation:

Given:

Tangent plane to a surface z=5x+2y-10 as the function at point (1,2)

To find :

f(x,y) at (1,2)

partial derivatives of function w.r.t. (x and y) and value of that function at given points.

Solution:(refer the attachment also)

Now we know that

the equation of tangent plane at given points to the surface is given by,

f(x1,y1,z1) and z=f(x,y)

z-z1=Fx(x1,y1)*(x-x1)+Fy(x1,y1)*(y-y1)

here Fx(x1,y1) and Fy(x1,y1) are the partial derivatives of x and y.

now

taking partial derivative w.r.t. x we get

Fx(x1`,y1)=
`(d)/(dx) (5x+2y-10)`

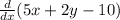
=5.

Then w.r.t y we get

Fy(x1,y1)=

`(d)/(dy)(5x+2y-10)`

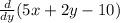
=2.

The values for Fx(1,2) and Fy(1,2) are 5 and 2 respectively.

Using the Linearization or linear approximation we get

L(x,y)=f(x1,y1)+Fx(x,y)*(x-x1)+Fy(x,y)(y-y1)

=-1+5(x-1)+2(y-2)

=5x+2y-10

Approximation at F(1.1,1.9)

=5(1.1)+2(1.9)-10

=5.5+3.8-10

=0.7

Approximation at points (1.1,1.9) is 0.7