Given Information:
Distribution = Poisson
Mean = 10
Required Information:
Expected number of stops = ?
Answer:
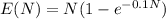
Explanation:
The number of people entering on the elevator is a Poisson random variable.
There are N floors and we want to find out the expected number of stops that the elevator will make before discharging all of its passengers.
Mean = μ = 10
The expected number of stops is given by
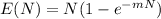
Where m is the decay rate and is given by
Decay rate = m = 1 /μ = 1/10 = 0.10
Therefore, the expected number of stops is
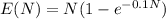
If we know the number of floor (N) then we can the corresponding expected value.