Question

Given the following information about a hypothesis test of the difference between two means based on independent random samples, which one of the following is the correct rejection region at a significance level of .05? Assume that the samples are obtained from normally distributed populations having equal variances.HA: μA > μB, = 12, = 9, s1 = 5, s2 = 3, n1 = 13, n2 = 10.A. Reject H0 if Z > 1.96B. Reject H0 if Z > 1.645C. Reject H0 if t > 2.08D. Reject H0 if t > 1.782E. Reject H0 if t > 1.721

Answer 1

Null hypothesis:
`\mu_(A) \leq \mu_(B)`

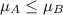
Alternative hypothesis:
`\mu_(A) > \mu_(B)`

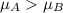
Since we dpn't know the population deviations for each group, for this case is better apply a t test to compare means, and the statistic is given by:

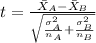`t=\frac{\bar X_(A)-\bar X_(B)}{\sqrt{(\sigma^2_(A))/(n_(A))+(\sigma^2_(B))/(n_(B))}}` (1)

Now we need to find the degrees of freedom given by:

`df = n_A + n_B -2= 13+10-2=21`

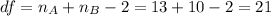
And now since we are conducting a right tailed test we are looking ofr a value who accumulates 0.05 of the are on the right tail fo the t distribution with df =21 and we got:

`t_(cric)= 1.721`

And for this case the rejection zone would be:

E. Reject H0 if t > 1.721

Explanation:

Data given and notation

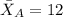`\bar X_(A)=12` represent the mean for 1

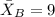`\bar X_(B)=9` represent the mean for 2

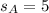`s_(A)=5` represent the sample standard deviation for 1

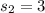`s_(2)=3` represent the sample standard deviation for 2

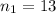`n_(1)=13` sample size for the group 1

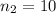`n_(2)=10` sample size for the group 2

t would represent the statistic (variable of interest)

`\alpha=0.05` significance level provided

Develop the null and alternative hypotheses for this study

We need to conduct a hypothesis in order to check if the mean for group A is higher than the mean for B:

Null hypothesis:
`\mu_(A) \leq \mu_(B)`

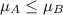
Alternative hypothesis:
`\mu_(A) > \mu_(B)`

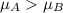
Since we dpn't know the population deviations for each group, for this case is better apply a t test to compare means, and the statistic is given by:

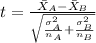`t=\frac{\bar X_(A)-\bar X_(B)}{\sqrt{(\sigma^2_(A))/(n_(A))+(\sigma^2_(B))/(n_(B))}}` (1)

Now we need to find the degrees of freedom given by:

`df = n_A + n_B -2= 13+10-2=21`

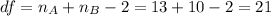
And now since we are conducting a right tailed test we are looking ofr a value who accumulates 0.05 of the are on the right tail fo the t distribution with df =21 and we got:

`t_(cric)= 1.721`

And for this case the rejection zone would be:

E. Reject H0 if t > 1.721