Answer:
Explanation:
Hello!
According to a study regarding the average age of female and male kids to complete toilet training is:
Females:
Average age 32.5 months
The standard deviation of 6.7 months
n= 126
Males:
Average age 35.0 months
The standard deviation of 10.1 months
n= 141
The parameter of study is the difference between the age of females are successfully toilet trained and the average age that males are successfully toilet trained. μf - μm (f= female and m= male)
a.
Assuming that both variables have a normal distribution to choose whether you'll use an unpooled or pooled-t to calculate the confidence interval you have to conduct an F-test for variance homogeneity.
If the variances are equal, then you can usee the pooled-t, but if the variances are different, you have to uses Wlche's approach:
H₀: δ²f = δ²m
H₁: δ²f ≠ δ²m
Since both items b. and c. ask for a 95% CI I'll use the complementary significance level for this test:
α: 0.05
Critical values:

The calculated F value is less than the lower critical value, 0.77, so the decision is to reject the null hypothesis. In other words, there is no significant evidence to conclude the population variances of the age kids are toilet trained to be equal. You should use Welch's approach to construct the Confidence Intervals.
b.
The given interval is:
[0.3627; 4.6073]
Using Welch's approach, the formula for the CI is:
(X[bar]f- X[bar]m) ±
 *
*
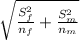
or
(X[bar]m- X[bar]f) ±
 *
*
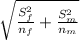
As you can see either way you calculate the interval, it is centered in the difference between the two sample means, so you can clear the value of that difference by:
(Upper bond - Lower bond)/2= (4.6073-0.3627)/2= 2.1223
The average age for females is 32.5 months and for males, it is 35 months.
Since the difference between the sample means is positive, we can say that the boys were considered "group 1" and the girls were considered "group 2"
You have a95% confidence that the parameter of interest is included in the given confidence interval.
c.
None of the statements is correct, the interval gives you information about the difference between the average age the kids are toilet trained, that is between the expected ages for the entire population of male and female babies.
This represents a guideline but is not necessarily true to all individuals of the population since some male babies can be toilet trained before that is expected as some female babies can be toiled trained after the average value.
I hope it helps!