Question

A gardener is planting two types of trees:

Type A is 10 feet tall and grows at a rate of 21 inches per year.
Type B is 7 feet tall and grows at a rate of 25 inches per year.
Algebraically determine exactly how many years it will take for these trees to be the
same height.​

Answer 1

9 years will take foe these trees to be the same height, If type A is 10 feet tall and grows at a rate of 21 inches per year and type B is 7 feet tall and grows at a rate of 25 inches per year.

Explanation:

The given is,

Type A is 10 feet tall and grows at a rate of 21 inches per year

Type B is 7 feet tall and grows at a rate of 25 inches per year

Step:1

Convert the rate of grows of tree inch to feet,

For Tree A,

Rate of grow, A = 21 inches per year

= 21 × 0.0833333 ( 1 inch = 0.0833333 feet)

= 1.75 feet per year

For Tree B,

Rate of grow, B = 25 inches per year

= 25 × 0.0833333 ( 1 inch = 0.0833333 feet)

= 2.08333 feet per year

Step:2

Difference in the tall of Tree A & B,

= 10 - 7

= 3 feet

Difference in the rate of grow of tree A & B,

= 2.08333 - 1.75

= 0.3333325 feet per year

Step:3

Year take to both trees are same height,

`= (Difference in the height of tree A & B)/(Difference in the rate of grows of A & B)`

`= (3)/(0.3333325)`

`= 9.00`

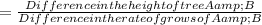
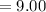
= 9 years

Step:4

Check for solution,

Height of tree = Height of Tree + (Rate of grow × Years)

For A,

= 10 + ( 1.75 × 9 )

= 25.75 feet.........................................(1)

For B,

= 7 + ( 2.08333 × 9 )

= 25.74999

≅ 25.75 feet.....................................(2)

From Equation (1) and (2),

25.75 feet = 25.75 feet

Result:

9 years will take foe these trees to be the same height, If type A is 10 feet tall and grows at a rate of 21 inches per year and type B is 7 feet tall and grows at a rate of 25 inches per year.