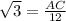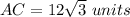Answer:
Part 1)
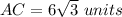
Part 2)
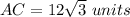
Explanation:
I will analyze two problems
see the attached figure to better understand the problem
Problem 1
The hypotenuse is the segment AB and the right angle is C
we know that
In the right triangle ABC
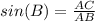 ---> by SOH (opposite side divided by the hypotenuse)
---> by SOH (opposite side divided by the hypotenuse)
substitute the given values
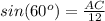
Remember that
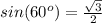
substitute

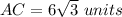
Problem 2
The hypotenuse is the segment BC and the right angle is A
we know that
In the right triangle ABC
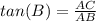 ---> by TOA (opposite side divided by the adjacent side)
---> by TOA (opposite side divided by the adjacent side)
substitute the given values
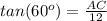
Remember that
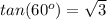
substitute