Question

LOTS OF POINTS IM DESPERATE! can someone please refresh my memory on a couple of log equations? Thank you!

Answer 1

78. t=8.66yrs

79. r=23.10%

80. r=11.0975%

Explanation:

78. Given the initial deposit is $1,000 and the 8% compounded continuously. The doubling time can be calculated using the formula;

`A=Pe^(it)`

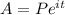
Given that A=2P, we substitute in the equation to solve for t:

`A=Pe^(rt)\\\\2P=Pe^(rt)\\\\2=e^(0.08t)\\\\0.08t=\ In 2\\\\t=8.66\ years`

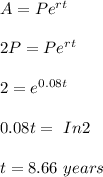
Hence, it takes 8.66 years for $1,000 to double in value.

79.

Given the initial deposit is $1,000 and the r% compounded continuously.

-The doubling rate can be calculated using the formula;

`A=Pe^(rt)`

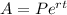
#We substitute our values in the equation to solve for r:

`A=Pe^(rt)\\\\A=2P, t=3\\\\\therefore\\\\2P=Pe^(3r)\\\\2=e^(3r)\\\\r=(In \ 2)/(3)\\\\=0.23105\approx 23.10\%`

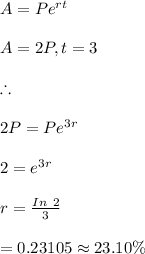
Hence, the deposit will double in 3 years at a rate of 23.10%

80.

Given the initial deposit is $30,000 and the future value is $2,540,689.

-Also, given t=40yrs, the rate of growth for continuous compounding is calculated as:

`A=Pe^(rt), \ \ \ r=r, t=40yrs\\\\2540689=30000e^(40r)\\\\(2540689)/(30000)=e^(40r)\\\\r=(In \ (2540689/30000))/(40)\\\\\\=0.110975=11.0975\%`

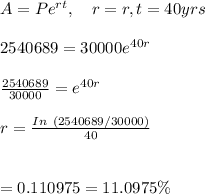
Hence, the deposit will grow at a rate of approximately 11.0975%