Question

Vehicles entering an intersection from the east are equally likely to turn left, turn right, or proceed straight ahead. If 50 vehicles enter this intersection from the east, use technology and the normal approximation to the binomial distribution to find the exact and approximate probabilities of the following. (Round your answers to four decimal places.) (a)

Answer 1

The probability that at least two-third of vehicles in the sample turn is 0.4207.

Explanation:

Let X = number of vehicles that turn left or right.

The proportion of the vehicles that turn is, p = 2/3.

The nest n = 50 vehicles entering this intersection from the east, is observed.

Any vehicle taking a turn is independent of others.

The random variable X follows a Binomial distribution with parameters n = 50 and p = 2/3.

But the sample selected is too large and the probability of success is close to 0.50.

So a Normal approximation to binomial can be applied to approximate the distribution of X if the following conditions are satisfied:

1. np ≥ 10
2. n(1 - p) ≥ 10

Check the conditions as follows:

`np=50* (2)/(3)=33.333>10\\\\n(1-p)=50* (1)/(3)= = 16.667>10`

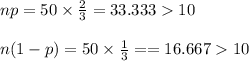
Thus, a Normal approximation to binomial can be applied.

So,
`X\sim N(np, np(1-p))`

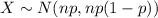
Compute the probability that at least two-third of vehicles in the sample turn as follows:

`P(X\geq (2)/(3)* 50)=P(X\geq 33.333)=P(X\geq 34)`

`=P((X-\mu)/(\sigma)>\frac{34-33.333}{\sqrt{50* (2)/(3)*\frac {1}{3}}})`

`=P(Z>0.20)\\=1-P(Z<0.20)\\=1-0.5793\\=0.4207`

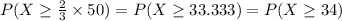
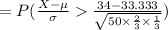
Thus, the probability that at least two-third of vehicles in the sample turn is 0.4207.