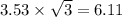Question

A right triangle has a hypotenuse of square root of 50. ​ What are possible lengths of the two legs of this triangle?

Answer 1

For 45-45-90 degree triangle

The length of other two legs: 5

For 30-60-90 degree triangle

The shorter leg= 3.53

The larger leg = 6.11

Explanation:

length of Hypotenuse =
`√(50)`

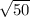
We need to find possible lengths of the two legs of this triangle.

If the triangle is 45-45-90 degree triangle the length of other two sides would be same and can be found by:

`Length\,\,of\,\,leg:(√(50) )/(√(2) ) \\Length\,\,of\,\,leg:5`

Since both legs are of same size so, length of other leg = 5

If the triangle is 30-60-90 degree triangle then:

To find shorter length: Divide hypotenuse by 2.

To find other side length: Multiply shorter length by
`√(3)`

The shorter leg =
`(√(50) )/(2)= 3.53`

The other leg (larger) =
`3.53* √(3) =6.11`