Answer:
the final speed of the 10.85 m/s.
Step-by-step explanation:
Given that,
Slope with respect to horizontal,

Distance travelled, d = 12 m
Initial speed of the cyclist, u = 9 m/s
We need to find the final speed of the cyclist. Let h is the height of the sloping surface such that,
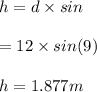
v is the final speed of the cyclist. It can be calculated using work energy theorem as
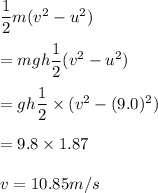
Thus,the final speed of the 10.85 m/s.