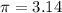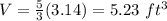Question

3. A balancing balloon toy is in the shape of a hemisphere (half-sphere) attached to the base of a cone. If the toy is 4ft tall and 2ft wide, what is the volume of the toy? Round your answer to two decimal places.

Answer 1

The volume of the toy is
`V=5.23\ ft^3`

Explanation:

step 1

Find the volume of the hemisphere

The volume of the hemisphere is given by the formula

`V=(2)/(3)\pi r^(3)`

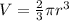
In this problem, the wide of the toy is equal to the diameter of the hemisphere

so

`D=2\ ft`

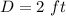
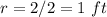`r=2/2=1\ ft` ----> the radius is half the diameter

substitute

`V=(2)/(3) \pi (1)^(3)=(2)/(3) \pi\ ft^3`

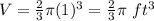
step 2

Find the volume of the cone

The volume of the cone is given by

`V=(1)/(3)\pi r^(2)h`

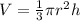
we know that

The radius of the cone is the same that the radius of the hemisphere

so

`r=1\ ft`

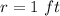
The height of the cone is equal to subtract the radius of the hemisphere from the height of the toy

`h=4-1=3\ ft`

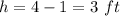
substitute the given values

`V=(1)/(3)\pi (1)^(2)(3)=\pi\ ft^3`

step 3

Find the volume of the toy

we know that

The volume of the toy, is equal to the volume of the cone plus the volume of the hemisphere.

so

`V=((2)/(3) \pi+\pi)\ ft^3`

`V=((5)/(3)\pi)\ ft^3`

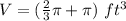
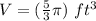
assume

`\pi=3.14`

`V=(5)/(3)(3.14)=5.23\ ft^3`