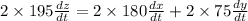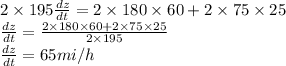Question

wo cars start moving from the same point. One travels south at 60 mi/h and the other travels west at 25 mi/h. At what rate is the distance between the cars increasing three hours later?

Answer 1

Answer: Both cars have equal kinetic energy

Step-by-step explanation:

Answer 2

`(dz)/(dt) = 65 mi/h`

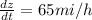
Step-by-step explanation:

let distance between two cars is = z mi

we have to find =
`(dz)/(dt)`

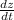
One travels south at = 60 mi/h =
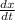`(dx)/(dt)` (given)

the other travels west at =25 mi/h.=
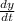`(dy)/(dt)\\` (given)

since both car have constant speed

at t = 3 hrs

x = 3× 60 = 180 mi/h

y = 3 × 25 = 75 mi/h

from the figure (i) we get

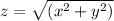`z = √(( x^2+ y^2))` ...............(i)

put x and y values

we get

`z = √((180)^2 + 75^2)`

`z = √(32400 + 5625) \\z = √(38025) \\z = 195 mi/h`

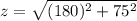
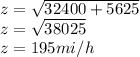
differentiate the equation (i) w r to t

`z^2 = x^2 +y^2`

`2z(dz)/(dt) = 2x(dx)/(dt)+ 2y(dy)/(dt)\\`

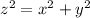
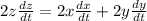
put each values

`2 *195(dz)/(dt) = 2 * 180(dx)/(dt)+2 *75(dy)/(dt)\\`

`2 *195(dz)/(dt) = 2 * 180* 60}+2 *75*25\\(dz)/(dt) = \frac{{2 * 180* 60+2 *75*25}}{ 2 *195}\\(dz)/(dt) = 65 mi/h`