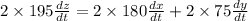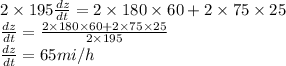Answer:
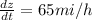
Step-by-step explanation:
let distance between two cars is = z mi
we have to find =
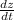
One travels south at = 60 mi/h =
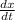 (given)
(given)
the other travels west at =25 mi/h.=
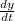 (given)
(given)
since both car have constant speed
at t = 3 hrs
x = 3× 60 = 180 mi/h
y = 3 × 25 = 75 mi/h
from the figure (i) we get
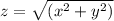 ...............(i)
...............(i)
put x and y values
we get
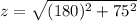
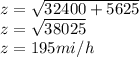
differentiate the equation (i) w r to t
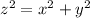
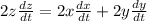
put each values