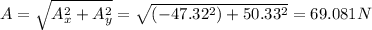Question

The uniform slender bar AB has a mass of 7 kg and swings in a vertical plane about the pivot at A. If angular velocity of the bar is 3 rad/s when θ = 35o , compute the force supported by the pin at A at that instant

Answer 1

The force supported by the pin at A is 69.081 N

Step-by-step explanation:

The diagram is in the figure attach. The angular acceleration using the moment expression is:

`-mg((Lcos\theta )/(2) )=I\alpha \\\alpha =(-3g)/(2L) cos\theta`

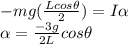
Where

L = length of the bar = 900 mm = 0.9 m

`\alpha =(-3*9.8cos35)/(2*0.9) =-13.38rad/s^(2)`

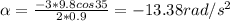
The acceleration in point G is equal to:

`a_(G) =a_(A) +\alpha kr_(G/A) -w^(2) r_(G/A)`

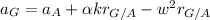
Where

aA = acceleration at A = 0

w = angular velocity of the bar = 3 rad/s

rG/A = position vector of G respect to A =
`(L)/(2) cos\theta i-(L)/(2) cos\theta j`

`a_(G) =((L)/(2)\alpha sin\theta -(w^(2)Lcos\theta )/(2) )i+((L)/(2)\alpha cos\theta +(w^(2)Lsin\theta )/(2) )j=((0.9*(-13.38)*sin35)/(2) -((3^(2)*0.9*cos35 )/(2) )i+((0.9*(-13.38)*cos35)/(2) +(3^(2) *0.9*sin35))/(2) )j=-6.76i-2.61jm/s^(2)`

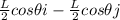
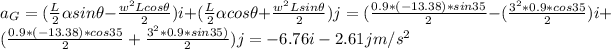
The force at A in x is equal to:

`A_(x) =ma_(G) =7*(-6.76)=-47.32N`

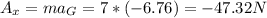
The force at A in y is:

`A_(y) =ma_(G) +mg=(7*(-2.61))+(7*9.8)=50.33N`

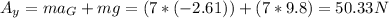
The magnitude of force A is equal to:

`A=\sqrt{A_(x)^(2)+A_(y)^(2) } =\sqrt{(-47.32^(2))+50.33^(2) } =69.081N`

Answer 2

49 N

Step-by-step explanation:

The diagram of the bar is obtained online and attached to this solution.

The free body diagram is also attached.

Since the weight of the bar acts at the middle of the bar, the torque due to the weight of the bar is given by

τ = mgx

where x = (L/2) cos 35° = 0.45 × cos 35° = 0.3686 m

τ = (7)(9.8)(0.3686) = 25.29 Nm

The force acting on pin A = torque ÷ (length × sin 35°) = 25.29 ÷ (0.9 × sin 35°)

= 25.29 ÷ 0.5162 = 48.99 N = 49 N

Hope this Helps!!!