Question

Two objects moving in opposite directions with the same speed v undergo a totally inelastic collision, and half the initial kinetic energy is lost. Find the ratio of their masses.

Answer 1

`(m)/(M) =((2)/(√(2) -1+1)) ^(-1)\\(m)/(M) =0.171572875`

Step-by-step explanation:

We name M the larger mas, and m the smaller mass, so base on this we write the following conservation of momentum equation for the collision:

`P_i=P_f\\M\,v_i -m\,v_i=(M+m)\,v_f\\(M-m)\,v_i = (M+m)\,v_f\\\\(v_i)/(v_f) = ((M+m))/((M-m))`

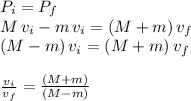
We can write this in terms of what we are looking for (the quotient of masses
`(m)/(M)`:

`(v_i)/(v_f) = ((1+(m)/(M) ))/((1-(m)/(M) ))`

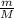We use now the information about Kinetic Energy of the system being reduced in half after the collision:

`K_i=2\,K_f\\(1)/(2) (M+m)\,v_i^2= 2*(1)/(2) (M+m)v_f^2\\v_i^2=2\,v_f^2\\(v_i^2)/(v_f^2) =2`

We can combine this last equation with the previous one to obtain:

`(v_i)/(v_f) = ((1+(m)/(M) ))/((1-(m)/(M) ))\\((v_i)/(v_f))^2 = ((1+(m)/(M) )^2)/((1-(m)/(M) )^2)\\2=((1+(m)/(M) )^2)/((1-(m)/(M) )^2)`

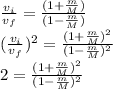
where solving for the quotient m/M gives:

`(m)/(M) =((2)/(√(2) -1+1)) ^(-1)\\(m)/(M) =0.171572875`