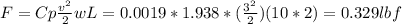Question

Find the shear stress and the thickness of the boundary layer (a) at the center and (b) at the trailing edge of a smooth flat plate 10 ft wide and 2 ft long parallel to the flow, immersed in 60F water (=1.938 slug/ft3, =1.217×10-5ft2/s =2.359×10-5 lbf.s/ft2) flowing at an undisturbed velocity of 3 ft/s. Assume laminar boundary layer over the whole plate. Also (f) find the total friction drag on one side of the plate.

Answer 1

a) The shear stress is 0.012

b) The shear stress is 0.0082

c) The total friction drag is 0.329 lbf

Step-by-step explanation:

Given by the problem:

Length y plate = 2 ft

Width y plate = 10 ft

p = density = 1.938 slug/ft³

v = kinematic viscosity = 1.217x10⁻⁵ft²/s

Absolute viscosity = 2.359x10⁻⁵lbfs/ft²

a) The Reynold number is equal to:

`Re=(1*3)/(1.217x10^(-5) ) =246507, laminar`

The boundary layer thickness is equal to:

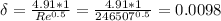`\delta=(4.91*1)/(Re^(0.5) ) =(4.91*1)/(246507^(0.5) ) =0.0098` ft

The shear stress is equal to:

`\tau=0.332((2.359x10^(-5)*3 )/(1) )(246507)^(0.5) =0.012`

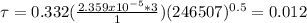
b) If the railing edge is 2 ft, the Reynold number is:

`Re=(2*3)/(1.215x10^(-5) ) =493015.6,laminar`

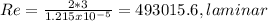
The boundary layer is equal to:

`\delta=(4.91*2)/(493015.6^(0.5) ) =0.000019ft`

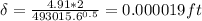
The sear stress is equal to:

`\tau=0.332((2.359x10^(-5)*3 )/(2) )(493015.6^(0.5) )=0.0082`

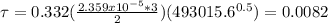
c) The drag coefficient is equal to:

`C=(1.328)/(√(Re) ) =(1.328)/(√(493015.6) ) ==0.0019`

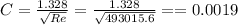
The friction drag is equal to:

`F=Cp(v^(2) )/(2) wL=0.0019*1.938*((3^(2) )/(2) )(10*2)=0.329lbf`