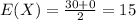Question

Rose and Jack plan to study together for the Math test. They decide to meet at the library between 8:00pm and 8:30pm. Assume that they each arrive (independently) at a random time (uniformly) in this interval. It is possible that someone has to wait up to 30 minutes for the other to arrive.

(a). What is the probability that someone (Rose or Jack, whichever arrives first) must wait more than 20 minutes until the other one arrives? What is the probability that Joe waits more than 20 minutes?

(b). What is the expected amount of time that somebody (the first person to arrive) waits? Formulate the problem and solve. Make sure you carefully define the random variables you use!

Answer 1

(a) 1/3

(b) 1/15

Explanation:

(a)Let X denote the waiting time in minutes. It is given that X follows a uniform distribution, and since the variable being measured is time, we assume it to be a continuous uniform distribution.

`\[f_X(x) =\begin{cases} (1)/(30) & 0\leqx\leq 30\\ 0 & otherwise \end{cases}\]`

Now

`P(X>20) = \int_(20)^(30)f_X(x) = (1)/(30) * 10 = (1)/(3)`.

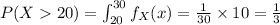Jack or Rose arriving first is equally likely, therefore the probability of Jack waiting is just the half of the above obtained probability i.e
`(1)/(6)`

(b)Using the formula for the expectation of a uniform continuous distribution,

`E(X) = (30+0)/(2) = 15`