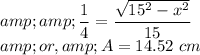Answer:
The value of the distance is
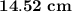 .
.
Step-by-step explanation:
The velocity of a particle(v) executing SHM is

where,
 is the angular frequency,
is the angular frequency,
 is the amplitude of the oscillation and
is the amplitude of the oscillation and
 is the displacement of the particle at any instant of time.
is the displacement of the particle at any instant of time.
The velocity of the particle will be maximum when the particle will cross its equilibrium position, i.e.,
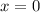 .
.
The maximum velocity(
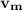 ) is
) is

Divide equation (1) by equation(2).

Given,
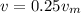 and
and
 . Substitute these values in equation (3).
. Substitute these values in equation (3).