Answer:
78 ml of 7% vinegar and 312 ml of 12% vinegar.
Explanation:
Let x represent ml of 7% vinegar brand and y represent ml of 12% vinegar brand.
We have been given that chef wants to make 390 milliliters of the dressing. We can represent this information in an equation as:
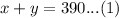
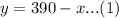
We are also told that 1st brand 7% vinegar, so amount of vinegar in x ml would be
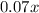 .
.
The second brand contains 12 vinegar, so amount of vinegar in y ml would be
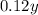 .
.
We are also told that the chef wants to make 390 milliliters of a dressing that is 11% vinegar. We can represent this information in an equation as:
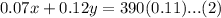
Upon substituting equation (1) in equation (2), we will get:
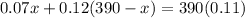
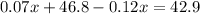

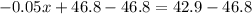
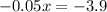

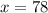
Therefore, the chef should use 78 ml of the brand that contains 7% vinegar.
Upon substituting
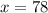 in equation (1), we will get:
in equation (1), we will get:
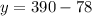
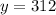
Therefore, the chef should use 312 ml of the brand that contains 12% vinegar.