Answer:
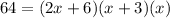
is the required equation for volume of box.
Explanation:
We are given the following in the question:
The box is
 inches wide.
inches wide.
Width, w =
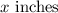
Height of box, h =
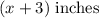
Length of box, l =
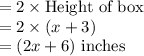
Volume of box = 64 cubic inches
Formula:

Putting values, we get,
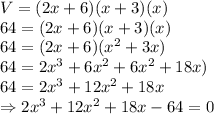
is the required equation.