Answer:
a) The volume of S is 34.13
b) The volume of S is 14.8
c) The volume of S is 5.17
d) The volume of S is 11.33
Explanation:
a) The cross section area is equal to:
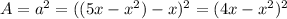
The volume of S is equal to:
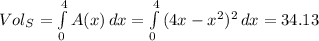
b) The cross section area is equal to:
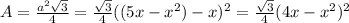
The volume of S is equal to:
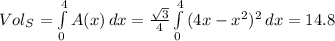
c)
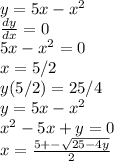
The cross section area is equal to:
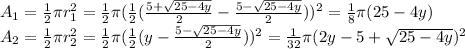
The volume of S is equal to:
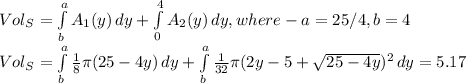
d) The cross section area is:
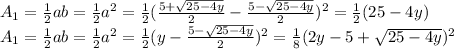
The volume of S is equal to:
