Answer:
The standard deviation of the number of defective bulbs produced in an hour is 6.615
Explanation:
Binomial probability distribution
Probability of exactly x sucesses on n repeated trials, with p probability.
The expected value of the binomial distribution is:
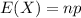
The standard deviation of the binomial distribution is:
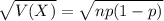
In this problem, we have that:
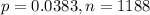
What is the standard deviation of the number of defective bulbs produced in an hour
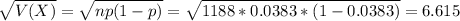
The standard deviation of the number of defective bulbs produced in an hour is 6.615