Question

A local soccer team has 6 more games that it will play. If it wins its game this weekend, then it will play its final 5 games in the upper bracket of its league, and if it loses, then it will play its final 5 games in the lower bracket. If it plays in the upper bracket, then it will independently win each of its games in this bracket with probability 0.3, and if it plays in the lower bracket, then it will independently win each of its games with probability 0.4. If the probability that it wins its game this weekend is 0.5, what is the probability that it wins at least 3 of its final 5 games?

Answer 1

Probability that it wins at least 3 of its final 5 games = .02387

Explanation:

Given -

The probability of win the weekend game = 0.5

The probability of loose the weekend game = 0.5

If he wins the game this weekend then it will play its final 5 games in the upper bracket of its league

In this case, probability of success is (p) = 0.3

probability of failure is (q) = 1 - p = 0.7

Let X be number of game won out of last five games

probability that it wins at least 3 of its final 5 games

( 1 )

`P(X\geq3)` =
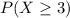`P(X\geq3/first\; game\; won)` ( probability of first game won )

=
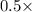`0.5*`P( X =3 ) +
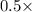`0.5*`P( X =4) +
`0.5* P(X = 5)`

=
`0.5*\binom{5}{3}(0.3)^(3)(0.7)^(2) + 0.5*\binom{5}{4}(0.3)^(4)(0.7)^(1)` +
`0.5*\binom{5}{5}(0.3)^(5)(0.7)^(0)`

=
`0.5*(5!)/((3!)(2!))*(0.3)^(3)*(0.7)^(2) + 0.5*(5!)/((4!)(1!))*(0.3)^(4)*(0.7)^(1)` +
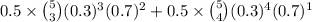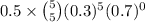
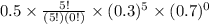`0.5*(5!)/((5!)(0!))*(0.3)^(5)*(0.7)^(0)`= = .065 + .014 + .001215 = .080

If he loose the game this weekend then it will play its final 5 games in the lower bracket of its league

In this case, probability of success is (s) = 0.4

probability of failure is (t) = 1 - s = 0.6

( 2 )

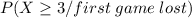`P(X\geq3/first\; game\; lost)` ( probability of first game lost )

=
`0.5* P(X = 3) + 0.5* P(X = 4)` +
`0.5* P(X=5)`

=
`\binom{5}{3}(0.4)^(3)(0.6)^(2) + 0.5*\binom{5}{4}(0.4)^(4)(0.6)^(1)`+
`0.5*\binom{5}{5}(0.4)^(5)(0.6)^(0)`

=
`0.5*(5!)/((3!)(2!))*(0.4)^(3)*(0.6)^(2) + 0.5*(5!)/((4!)(1!))*(0.4)^(4)*(0.6)^(1)` +
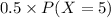
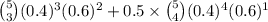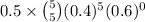
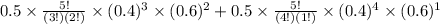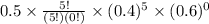`0.5*(5!)/((5!)(0!))*(0.4)^(5)*(0.6)^(0)` = = .1152 + .0384 + .00512 = .1587

Required probability = ( 1 ) + ( 2 ) = .02387