Question

A satellite is in a circular orbit around the Earth at an altitude of 3.58 106 m. (a) Find the period of the orbit. (Hint: Modify Kepler's third law so it is suitable for objects orbiting the Earth rather than the Sun. The radius of the Earth is 6.38 106 m, and the mass of the Earth is 5.98 1024 kg.)

Answer 1

The period of the orbit is
`9.88* 10^3\ s`.

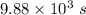Step-by-step explanation:

Given that,

A satellite is in a circular orbit around the Earth at an altitude of,
`h=3.58* 10^6\ m`

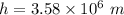
We need to find the period of the orbit. It can be calculated using Kepler's law. It is given by :

`T^2\propto a^3\\\\T^2=(4\pi^2)/(Gm)a^3`

a is distance of semi major axis, a = h+ r, r is radius of earth

m is mass of earth

So,

`T^2=(4\pi^2)/(Gm)(r+h)^3\\\\T^2=(4\pi^2)/(6.67* 10^(-11)* 5.98* 10^(24))(6.38* 10^6+3.58* 10^6)^3\\\\T=9.88* 10^3\ s`

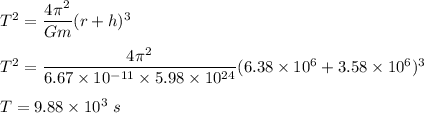
So, the period of the orbit is
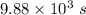`9.88* 10^3\ s`.