Answer:
The bridge's height above the water is 130 feets.
Explanation:
A rock is thrown upward from a bridge into a river below :
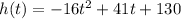
Here t is time in seconds
It is required to find the bridge's height above the water. When it reaches the height of the rock above the surface of the water, then :
h(t) = 0
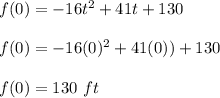
So, the bridge's height above the water is 130 feets.