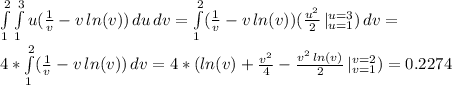Question

Let R be the region in the first quadrant of the​ xy-plane bounded by the hyperbolas xyequals​1, xyequals9​, and the lines yequals​x, yequals4x. Use the transformation x equals StartFraction u Over v EndFraction ​, y equals uv with ugreater than0 and vgreater than0 to rewrite the integral below over an appropriate region G in the​ uv-plane. Then evaluate the​ uv-integral over G.

Answer 1

To rewrite the integral over an appropriate region G in the​ uv-plane, we need to use the given transformation x = u/v and y = uv. The region G is defined by certain constraints on u and v, which can be found by solving the inequalities derived from the boundaries of R in the xy-plane. Finally, we can set up and evaluate the double integral over G.

Step-by-step explanation:

To rewrite the integral over an appropriate region G in the​ uv-plane, we need to use the given transformation x = u/v and y = uv. Let's consider each boundary of R separately:

1. For the hyperbola xy = 1, substituting the given transformations, we get (u/v)(uv) = 1, which simplifies to u^2 = v.
2. For the hyperbola xy = 9, substituting the given transformations, we get (u/v)(uv) = 9, which simplifies to u^2 = 9v.
3. For the line y = x, substituting the given transformations, we get uv = u/v.
4. For the line y = 4x, substituting the given transformations, we get uv = 4(u/v).

Now, we need to find the region G in the uv-plane that corresponds to R in the xy-plane. The region G is defined by the following constraints: u^2 ≤ v, 9v ≥ u^2, uv ≤ u/v, and uv ≥ 4(u/v). Combining these constraints, we get u^4 ≤ v^2 ≤ 9u^3 and u^2 ≤ 4v. The boundaries of G can be found by solving these inequalities.

To evaluate the integral over G, we need to determine the limits of integration for u and v. Once we have the limits, we can set up the double integral of the function over G and evaluate it.

Answer 2

The area can be written as

`\int\limits_1^2 \int\limits_1^3 u((1)/(v) - v \, ln(v)) \, du \, dv = 0.2274`

And the value of it is approximately 1.8117

Step-by-step explanation:

x = u/v

y = uv

Lets analyze the lines bordering R replacing x and y by their respective expressions with u and v.

• x*y = u/v * uv = u², therefore, x*y = 1 when u² = 1. Also x*y = 9 if and only if u² = 9

• x=y only if u/v = uv, And that only holds if u = 0 or 1/v = v, and 1/v = v if and only if v² = 1. Similarly y = 4x if and only if 4u/v = uv if and only if v² = 4

Therefore, u² should range between 1 and 9 and v² ranges between 1 and 4. This means that u is between 1 and 3 and v is between 1 and 2 (we are not taking negative values).

Lets compute the partial derivates of x and y over u and v

`x_u = 1/v`

`x_v = u*ln(v)`

`y_u = v`

`y_v = u`

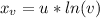
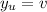
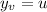
Therefore, the Jacobian matrix is

`\left[\begin{array}{ccc}(1)/(v)&u \, ln(v)\\v&u\end{array}\right]`

and its determinant is u/v - uv * ln(v) = u * (1/v - v ln(v))

In order to compute the integral, we can find primitives for u and (1/v-v ln(v)) (which can be separated in 1/v and -vln(v) ). For u it is u²/2. For 1/v it is ln(v), and for -vln(v) , we can solve it by using integration by parts:

`\int -v \, ln(v) \, dv = - ((v^2 \, ln(v))/(2) - \int (v^2)/(2v) \, dv) = (v^2)/(4) - (v^2 \, ln(v))/(2)`

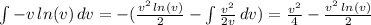
Therefore,

`\int\limits_1^2 \int\limits_1^3 u((1)/(v) - v \, ln(v)) \, du \, dv = \int\limits_1^2 ((1)/(v) - v \, ln(v) ) ((u^2)/(2)\, |_(u=1)^(u=3)) \, dv= \\4* \int\limits_1^2 ((1)/(v) - v\,ln(v)) \, dv = 4*(ln(v) + (v^2)/(4) - (v^2\,ln(v))/(2) \, |_(v=1)^(v=2)) = 0.2274`