Question

A company borrowed $40,000 for 3 years at 6% compounded daily. It will not make any payments on this loan prior to maturity. Find (a) the total future value they will need to accumulate to pay off this debt, and (b) the quarterly sinking fund payment needed to accumulate this maturity value, assuming a 5% rate.

Answer 1

a A=$47,887.81

b.A=$46,430.80

Explanation:

a. Given the initial amount is $40,000 with a 3-year term and a 6% rate compounded daily.

-Take 1 year=365 days

#First we calculate the effective interest rate corresponding to the daily compounding;

`i_m=(1+i/m)^m-1\\\\=(1+0.06/365)^(365)-1\\\\=0.06183`

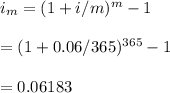
#We use the calculated effective rate, 0.06183, to solve for the future value as:

`A=P(1+i_m)^n\\\\=40000(1.06183)^3\\\\=47887.81`

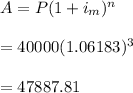
Hence, the total future value for a daily compounding is $47,887.81

b. For a sinking fund with a 5% compounded quarterly:

#We calculate the annual effective rate:

`i_m=(1+i/m)^m-1\\\\=(1+0.05/4)^4-1\\\\=0.05095`

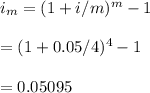
#We use the calculated effective rate, 0.05095, to solve for the future value as:

`A=P(1+i_m)^n\\\\=40000(1.05095)^3\\\\=46430.80`

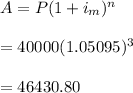
Hence, the future value of the sinking fund is $46,430.80