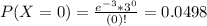Answer:
0.0498 = 4.98%
Explanation:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given time interval.
is the mean in the given time interval.
Inquiries arrive at a record message device according to a Poisson process of rate 15 inquiries per minute.
Each minute has 60 seconds.
So a rate of 1 inquire each 4 seconds.
The probability that it takes more than 12 seconds for the first inquiry to arrive is approximately
Mean of 1 inquire each 4 seconds, so for 12 seconds

This probability is P(X = 0).