Question

He takes a random sample of 49 recent charterholders and computes a mean salary of $172,000 with a standard deviation of $35,000. Use this sample information to determine the 90% confidence interval for the average salary of a CFA charterholder.

Answer 1

the 90% of confidence intervals for the average salary of a CFA charter holder

(1,63,775 , 1,80,000)

Explanation:

Explanation:-

random sample of n = 49 recent charter holders

mean of sample (x⁻) = $172,000

standard deviation of sample( S) = $35,000

Level of significance α= 1.645

90% confidence interval

`(x^(-) - Z_(\alpha ) (s)/(√(n) ) , x^(-) + Z_(\alpha ) (s)/(√(n) ))`

`(172000 - 1.645 (35000)/(√(49) ) , 172000 +1.645 (35000)/(√(49) ))`

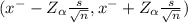
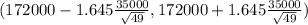
on calculation , we get

(1,63,775 , 1,80,000)

The mean value lies between the 90% of confidence intervals

(1,63,775 , 1,80,000)