Question

F the angle of elevation from the point on the ground to the top of the tree is 34° and the point is 25 feet from the base of the tree, what is the height of the tree (to the nearest tenth of a foot)?

A) 14.0 feet
B) 16.9 feet
C) 19.3 feet
D) 20.7 feet

Answer 1

16.9 feet

Explanation:

Answer 2

Given:

The angle of elevation from the point on the ground to the top of the tree is 34° and the point is 25 feet from the base of the tree.

We need to determine the height of the tree.

Height of the tree:

Let the height of the tree be h.

The height of the tree can be determined using the trigonometric ratio.

Thus, we have;

`tan \ \theta=(opp)/(adj)`

Substituting the values, we get;

`tan \ 34^(\circ)=(h)/(25)`

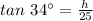
Multiplying both sides by 25, we have;

`tan \ 34^(\circ) * 25=h`

`0.6745 * 25=h`

`16.8625=h`

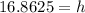
Rounding off to the nearest tenth of a foot, we get;

`16.9=h`

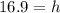
Thus, the height of the tree is 16.9 feet.

Hence, Option B is the correct answer.