Answer:
a) Work done on the astronaut by the force from the helicopter = 16.104 kJ
b) Work done on the astronaut by the gravitational force = -15.082 kJ
Step-by-step explanation:
mass of the astronaut, m = 81 kg
height, h = 19 m
acceleration of the astronaut, a = g/15
Since the astronaut is lifted up, using the third law of motion:
T - mg = ma
T = mg + ma
T = (81*9.81) + 81*(9.81/15)
T = 847.584 N
Work done on the astronaut by the helicopter
Work done = Tension * height
W = T* h
W = 847.584 * 19
Work done, W = 16104.096 Joules
W = 16.104 kJ
b) Work done on the astronaut by the gravitational force on her

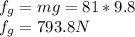
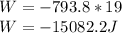
W = -15.082 kJ