Answer:
V =
 π(8 -
π(8 -
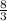 )
)
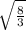 = 9.11
= 9.11

r = 4
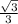
h =
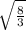
Explanation:
Given that the right triangle whose hypotenuse is

- Let r is the radius of the cone
- Let h is the height of the cone
We know that:
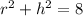
<=>
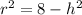
The volume of the cone is:
V = π
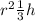
<=> V = π

Differentiate w.r.t h
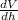 = π
= π
 (8 -
(8 -
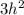 )
)
For maximum/minimum:
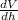 = 0
= 0
<=> π
 (8 -
(8 -
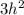 ) = 0
) = 0
<=>
 =
=
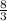
<=> h =
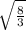
=>
 =
=
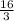
<=> r = 4
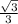
So the volume of the cone is:
V =
 π(8 -
π(8 -
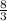 )
)
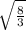 = 9.11
= 9.11
