Question

In your job at the container factory, you are asked to design a rectangular box with volume 500 cm3 . The material for the sides and bottom costs $0.05 per cm2 while the material for the top costs $0.15 per cm2 . What dimensions do you recommend to minimize the total material cost

Answer 1

6.3 cm by 6.3 cm by 12.6cm

Explanation:

Volume of the box=
`500 cm^3`

The minimal dimensions of a box always occur when the base is a square.

`L^2H=`
`500 cm^3`

`H=(500)/(L^2)`

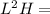
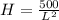
Surface Area of a cylinder=
`2(L^2+LH+LH)`

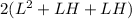
Surface Area of the sides and bottom=
`L^2+2(LH+LH)`

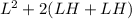
Surface Area for the top =
`L^2`

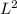
The material for the sides and bottom costs $0.05 per
`cm^2`

The material for the top costs $0.15 per
`cm^2`

Therefore Cost of the box

`C=0.15L^2+0.05[L^2+4LH]\\C=0.2L^2+0.2LH`

Recall:
`H=(500)/(L^2)`

`C=0.2L^2+0.2L((500)/(L^2))\\=0.2L^2+(100)/(L)\\C=(0.2L^3+100)/(L)`

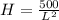
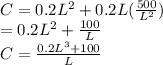
The minimum value of C is at the point where the derivative is zero.

`C^(')=(2(L^3-250))/(5L^2)\\(2(L^3-250))/(5L^2)=0\\2(L^3-250)=0\\L^3=250\\L=6.3cm`

`H=(500)/(L^2)=(500)/(6.3^2)=12.6cm`

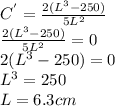
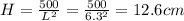
The dimensions that would minimize the cost are 6.3 cm by 6.3 cm by 12.6cm