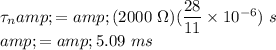Answer:
The resulting time constant will be
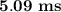 .
.
Step-by-step explanation:
Given:
the time constant of the RC circuit,
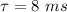
The value of the capacitor in the circuit,
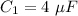
The value of addition capacitor added to the circuit,
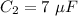
The value of the time constant for a series RC circuit is give by
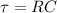
So the value of the resistance in the circuit is
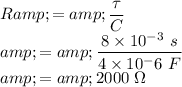
When the capacitor
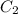 is added to the circuit, the net value of the capacitance in the circuit is
is added to the circuit, the net value of the capacitance in the circuit is
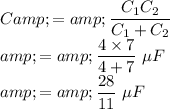
So the new time constant will be