Answer:
Required conclusion is that if
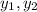 satisfies given differential equation and wronskean is zero then they are considered as solution of that differential equation.
satisfies given differential equation and wronskean is zero then they are considered as solution of that differential equation.
Explanation:
Given differential equation,
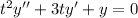

(i) To verify
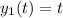 is a solution or not we have to show,
is a solution or not we have to show,
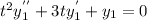
But,
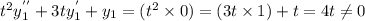
hence
 is not a solution of (1).
is not a solution of (1).
Now if
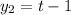 is another solution where
is another solution where
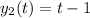 then,
then,
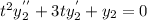
But,
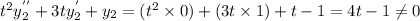
so
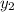 is not a solution of (1).
is not a solution of (1).
(ii) Rather the wronskean,
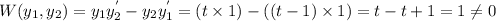
Hence it is conclude that if
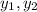 satisfies (i) along with condition (ii) that is wronskean zero, only then
satisfies (i) along with condition (ii) that is wronskean zero, only then
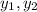 will consider as solution of (1).
will consider as solution of (1).