Question

At the instant when the speed of the loop is 3.00 m/sm/s and it is still partially in the field region, what is the magnitude of the force that the magnetic field exerts on the loop?

Answer 1

Complete Question:

A rectangular loop of wire with dimensions 1.50 cm by 8.00 cm and resistance 0.700 Ω is being pulled to the right out of a region of uniform magnetic field. The magnetic field has magnitude 2.20 T and is directed into the plane of.

At the instant when the speed of the loop is 3.00 m/s and it is still partially in the field region, what is the magnitude of the force that the magnetic field exerts on the loop?

Answer:

F = 0.133 N

Step-by-step explanation:

Magnitude of the magnetic field, B = 2.20 T

Length of the loop = 1.5 cm = 0.015 m

The speed of the loop, v = 3.00 m/s

The emf induced in the loop , e = Blv

e = 2.20 * 0.015 * 3

e = 0.099 V

Current induced in the loop, I = e/R

I = 0.099/0.7

I = 0.1414 A

The magnitude of the force is given by, F = I *l *B sin90

F = 0.1414 * 0.015 * 2.20

F = 0.00467 N

Answer 2

Complete question:

A rectangular loop of wire with dimensions 2.0 cm by 10.0 cm and resistance 1.0 Ω is being pulled to the right out of a region of uniform magnetic field. The magnetic field has magnitude of 2.0 T and is directed into the plane. At the instant when the speed of the loop is 3.00 m/s and it is still partially in the field region, what is the magnitude of the force that the magnetic field exerts on the loop?

Check the image uploaded

Answer:

The magnitude of the force that the magnetic field exerts on the loop 4.8 x 10⁻³ N

Step-by-step explanation:

Given;

resistance of the wire; R = 1.0 Ω

magnitude of magnetic field strength, B = 2.0 T

speed of the loop, v = 3.00 m/s

Induced emf is given as;

ε = IR

`I = (emf)/(R) = (VBL)/(R)`

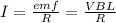
magnitude of the force that the magnetic field exerts on the loop:

F = BIL

Substitute in the value of I

`F = (VB^2L^2)/(R)`

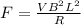
where;

L is the displacement vector between the initial and final end of the portion of the wire inside the field = 2.0 cm

Substitute the given values and solve for F

`F = (3*2^2*(2*10^(-2))^2)/(1) \\\\F = 4.8 *10^(-3) \ N`

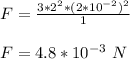
Therefore, the magnitude of the force that the magnetic field exerts on the loop 4.8 x 10⁻³ N