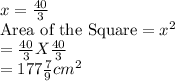Question

An open-top box is to be made from a 70-centimeter by 96-centimeter piece of plastic by removing a square from each corner of the plastic and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume? Enter the area of the square and do not include any units in your answer. Enter an improper fraction if necessary.

Answer 1

`177 (7)/(9) cm^2`

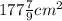
Explanation:

Length of the Plastic Sheet= 96cm

Width of the plastic Sheet =70cm

If a square of side x is cut from each corner of the plastic sheet to form the box.

Length of the box=96-2x

Width of the box=70-2x

Height of the box =x

Volume of the box = LWH

Volume=(96-2x)(70-2x)x

The maximum volume of the box is obtained at the point where the derivative is zero.

`V=(96-2x)(70-2x)x\\V^(')=4(x-42)(3x-40)`

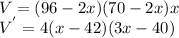
Setting the derivative to 0.

`4(x-42)(3x-40)=0\\x-42=0\: 3x-40=0\\x=42\:or\: x=(40)/(3)`

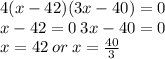
Since we are looking for the minimum value of x,

`x=(40)/(3)\\\text{Area of the Square} = x^2\\=(40)/(3) X (40)/(3)\\=177 (7)/(9) cm^2`