Question

(a) For what frequencies does a 23.0-μF capacitor have a reactance below 160 Ω? f Correct: Your answer is correct. 6.95 Incorrect: Your answer is incorrect. Hz (b)What is the reactance of a 41.0-μF capacitor over this same frequency range? Xc Correct: Your answer is correct. Ω

Answer 1

(a) So range of frequency
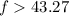`f > 43.27` Hz

(b) the reactance is 89.75 Ω

Step-by-step explanation:

Given:

(a)

Capacitance of a capacitor
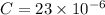`C= 23 * 10^(-6)` F

Reactance of capacitive circuit
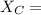`X_(C) =` 160 Ω

From the formula of reactance,

`X_(C) = (1)/(\omega C)`

`X_(C) = (1)/(2\pi fC)`

`f = (1)/(2\pi X_(C) C )`

`f = (1)/(6.28 * 160 * 23 * 10^(-6) )`

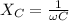
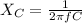
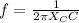
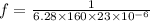
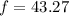`f = 43.27` Hz

So range of frequency
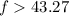`f > 43.27` Hz

(b)

Capacitance
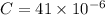`C = 41 * 10^(-6)` F

Frequency
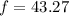`f = 43.27` Hz

From the formula of reactance,

`X_(C) = (1)/(2\pi fC)`

`X_(C) = (1)/(6.28 * 43.27 * 41 * 10^(-6) )`

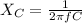
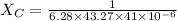
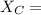`X_(C) =` 89.75 Ω

Therefore, the reactance is 89.75 Ω