Answer:
Their total self-inductance assuming they act like a single solenoid is 10.11 μH
Step-by-step explanation:
Given;
diameter of the heating coil, d = 0.800 cm
combined length of heating coil and hair dryer,
 = 1.0 m
= 1.0 m
number of turns, N = 400 turns
Formula for self-inductance is given as;
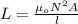
where
μ₀ is constant = 4π x 10⁻⁷ T.m/A
A is the area of the coil:
A = πd²/4
A = π (0.8 x 10⁻²)²/4
A = 5.027 x 10⁻⁵ m²
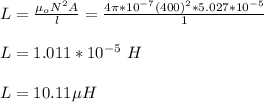
Therefore, their total self-inductance assuming they act like a single solenoid is 10.11 μH