Question

From an airplane at an altitude of 1400 meters, the angle of depression to a rock on the ground measures 31°. Find the direct line distance from the plane to the rock. Round to the nearest tenth of a meter.

Answer 1

1633.3 meters

Explanation:

-Given the angle of depression is 31°, and the plane's height above the ground is 1400m.

-We use the Law of Sines to determine the distance between the plane and the rock.

-The angle of elevation from the rock to the plane is(corresponds to the plane's altitude):

`\angle elevation=90-31\\=51\textdegree`

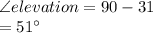
#Now, using Sine Law;

`(a)/(Sin \A)=(b)/(Sin \ B)\\\\\\(1400)/(Sin \ 59)=(d)/(Sin \ 90)\\\\\\\\=1633.287\approx 1633.3\ m`

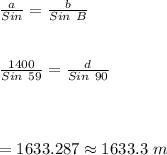
Hence, the direct distance between the plane and the rock is 1633.3 meters