Question

The wait times in line at a grocery store are roughly distributed normally with an average wait time of 7.6 minutes and a standard deviation of 30 seconds. What is the probability that the wait time is between 6 and 7.3 minutes

Answer 1

the probability that the wait time is between 6 and 7.3 minutes = 0.725

Explanation:

Given -

Average wait time
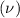`(\\u)` = 7.6 minutes

Standard deviation
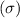`(\sigma)` = 30 second = .5 minute

Let X be the wait times in line at a grocery store

the probability that the wait time is between 6 and 7.3 minutes

[ Put z =
`(X - \\u )/(\sigma)` ]

`P (7.3> X>6 )` =
`P ((7.3 - 7.6)/(.5)> Z>(6 - 7.6 )/(.5) )`

=
`(.6> Z> -3.2 )`

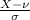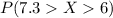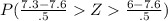
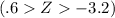
[Using z table]

= Area to the left of z = .6 - area to the left of z = -.32

= .7257 - .0007 = 0.725