Question

A Corporation offers a 5.8 percent bond with a current market price of $823.50. The yield to maturity is 8.18 percent. The face value is $1,000. Interest is paid semiannually. How many years until this bond matures

Answer 1

Step-by-step explanation:

First of all, as the interest is paid semi-annually, we calculate semi-annual interest rate by dividing yield to maturity by the number of periods in a year (2).

Semi-annual interest rate = 0.0818 / 2 = 0.0409

Now using the following formula

`YTM\;=\;\sqrt[n]{(Face\;Value)/(Current\;Price)}\;-\;1`

where,

YTM = 0.0409 (semi-annually)

Face Value = $1000

Current Price = $823.5

n = Number of semi-annual periods

`0.0409\;=\;\sqrt[n]{(1000)/(823.5)}\;-\;1\\\\0.0409\;+\;1=\;\sqrt[n]{{1.214}}\\\\1.0409^(n) =\;1.214\\\\`

Taking natural log on both sides,

`ln(1.0409)^(n) =ln(1.214)\\\\n*ln(1.0409)=ln(1.214)\\\\n=(ln(1.214))/(ln(1.0409))\\n=4.837`

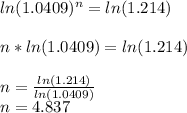
Hence, semi-annual periods are 4.837. Therefore, the bond will mature in approximately (4.837/2) 2.4185 years.