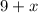Question

The rectangle below has an area of 81-x^2 square meters and a width of 9-x meters. What expression represents the length of the rectangle?

Answer 1

For this case we have that by definition, the area of a rectangle is given by:

`A = w * l`

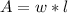
Where:

w: Is the width of the rectangle

l: is the length of the rectangle

According to the data of the statement we have:

`A = 81-x ^ 2\\w = 9-x`

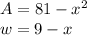
So, the length is given by:

`l = \frac {A} {w}\\l = \frac {81-x ^ 2} {9-x}`

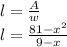
We factor the numerator:

`l = \frac {(9 + x) (9-x)} {9-x}`

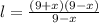
We simplify:

`l = 9 + x`

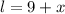
So, the length is
`9 + x`

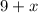
Answer:

`9 + x`